線性范圍的評估及數據處理方法
實驗樣本的基本要求和制備方法
基本要求
樣本基質應與臨床實驗樣本相似,但不可采用含有對測定方法具有明確干擾作用物質的樣本,如溶血、脂血、黃疸或含有某些特定藥物的樣本。進行血清學標志物檢測時,理想的樣本為分析物濃度接近預期測定上限的混合人血清。
建立一種定量測定方法的線性范圍時,需在預期測定范圍內選擇7-11個濃度水平。如將預期測定范圍加寬至130%,在此范圍內選擇更多的濃度水平,然后依據實驗結果逐漸減少數據點直至表現出線性關系,可發現最寬的線性范圍。
當對標稱線性參數進行驗證時,需在已知線性范圍內選擇5-7個濃度水平。
無論是建立或驗證線性范圍,所選用的濃度水平應可覆蓋整個預期測定范圍并包括與臨床有關的重要評價濃度,如最小測定濃度或線性范圍的最低限、不同的醫學決定水平、最大測定濃度或線性范圍的高限等。
制備方法
不同濃度水平的樣本可通過將高濃度樣本與低濃度樣本進行倍比稀釋得到,注意在進行液體吸取時應選擇精密度與準確性好的移液裝置。制備時應將樣本完全混合并避免蒸發或其他使樣本變質的情況。每份樣本的濃度與體積單位應統一。
如果高/低濃度血清的值未知,可將每種血清編碼,用編碼代表每個血清的相對濃度。對于等濃度間隔樣本,可用連續整數(如1、2、3、4、5)代表連續樣本。進行數據處理時可用樣本號代替X值。表1和表2中描述的樣本制備過程是按照等濃度間隔的設計進行的,每個濃度水平的樣本量為1.00ml。
表1:11個濃度水平的樣本制備
| 樣本號 | 1 | 2 | 3 | 4 | 5 | 6 |
| 低濃度血清(ml) | 1.00 | 0.90 | 0.80 | 0.70 | 0.60 | 0.50 |
| 高濃度血清(ml) | 0.00 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| 樣本號 | 7 | 8 | 9 | 10 | 11 | |
| 低濃度血清(ml) | 0.40 | 0.30 | 0.20 | 0.10 | 0.00 | |
| 高濃度血清(ml) | 0.60 | 0.70 | 0.80 | 0.90 | 1.00 |
表2:5個濃度水平的樣本制備
| 樣本號 | 1 | 2 | 3 | 4 | 5 |
| 低濃度血清(ml) | 1.00 | 0.75 | 0.50 | 0.25 | 0.00 |
| 高濃度血清(ml) | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 |
制備非等濃度間隔的樣本時應明確各樣本間的濃度關系,測定時可以這些樣本間的相對濃度比值做為X值。
樣本的特殊處理:在無法得到適用的人血清時,需對樣本進行一些特殊處理以滿足實驗要求。這些處理過程包括稀釋、加入添加物或透析、熱處理等,無論進行何種處理均應以保持基質恒定為基本原則。在評價報告中應對所使用的稀釋液、添加物、溶劑等的材料來源加以注明。
樣本稀釋液應選用由廠家推薦或經實驗室證明可使用的產品,如可采用5%牛血清白蛋白或人白蛋白溶液。欲提高樣本濃度時可在樣本中添加分析物純品。在添加物為溶液狀態時,應注意添加液體對樣本的稀釋作用(小于10%)并注明所用溶劑。
實驗過程
- 建立線性范圍:需測定9-11個濃度水平,每個濃度水平重復測定3-4次。
- 驗證標稱線性參數:需測定4-6個濃度水平,每個濃度水平重復測定3-4次。
- 所有樣本應在一次運行中或幾次間隔很短的運行中隨機測定,最好在一天之內完成。
數據處理
數據記錄
可參考下表進行數據記錄,也可采用其它形式進行記錄,但應注意保留原始數據。
| 項目: | 樣品: | ||||
| 儀器: | 試劑/批號: | 校準品/批號: | |||
| 操作者: | 審核者: | 測定日期: | |||
| 樣本號 | 測定1 | 測定2 | 測定3 | 測定4 | 均值 |
| 1 | |||||
| 2 | |||||
數據可用性檢查
可通過繪制散點圖對測定數據的可用性進行初步檢查。以樣本號或樣本濃度為X軸,以測定結果為Y軸做圖,在圖上標出針對每個樣本的測定值及每個濃度水平的測定均值,手工或用計算機做圖將均值點相連,觀察數據點與直線間的偏差,如偏差過大,表明數據組存在明顯非線性,需要對測定過程進行檢查,排除因操作錯誤所至誤差,并對樣本進行重新測定。如圖形與直線接近,表明可對數據組繼續進行統計分析。
剔除離群值
離群值可由散點圖初步判斷,標準中建議采用格拉布斯(GRUBBS)法進行離群值檢驗。檢驗步驟如下:
- 1. 每組數據中有4個測定結果,分別記為 y1,y2,y3,y4。
- 2. 將4個測定值按大小順序排列,最大值記為max,最小值記為 min;
- 3. 由4個測定值計算均值y和標準差S:
y=(y1+y2+y3+y4)/4;
- 4. 根據可疑值 max或 min分別按下式計算統計量t:
t1 = (max-)/S,t2 = (min-)/S; - 5. 根據給定的顯著性水平a和重復測定次數查表得臨界值,如t值大于臨界值,則相應的可疑值為離群值。
進行多項回歸分析
對數據組進行多項回歸分析,得到一級、二級與三級多項式。一級多項式為直線,二級多項式表示上升曲線或下降曲線,三級多項式表示S形曲線(在測量范圍兩端具有明顯的非線性)。多項式方程如下:
| 級數 | 多項式 | 回歸自由度(Rdf) |
|---|---|---|
| 一級 | Y = b0 + b1X | 2 |
| 二級 | Y = b0 + b1X + b2X2 | 3 |
| 三級 | Y = b0 + b1X + b2X2 + b3X3 | 4 |
對回歸方程進行線性檢驗
多元回歸方程中以bi表示的系數為回歸系數。在二級與三級方程中,b2與b3為非線性系數。對回歸方程進行線性檢驗就是對每個非線性系數作t檢驗,判斷回歸系數與零是否有顯著性差異。b0與b1不反映非線性,故不需對其進行檢驗。對b2與b3的檢驗方法如下:
計算統計量t,計算公式為:
t = bi/ SEi
式中SEi 為每個非線性系數的斜率標準誤,計算公式為:
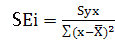 ;
;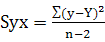 ;
;
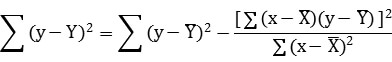 ;
;
其中,Y為回歸方程預測值, 與
與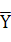 與為測定均值。
與為測定均值。
由公式df = L*R-Rdf 計算自由度,L為樣本數,R為每個樣本的測定次數,Rdf為回歸自由度,即回歸方程中系數(包括b0)的個數。如測定5樣本,每個樣本重復測定4次,則對測定數據進行回歸分析后其三級多項式中L=5,R=4,Rdf=4,df=5*4-4=16。在t值表中尋找t界值(雙邊檢驗,α=0.05),將計算出的t值與界值比較,如p>0.05,表示非線性系數與零無顯著性差異,數據組被認為具線性,此時可對數據組進行精密度檢驗,具體方法見后。當精密度符合線性判斷要求時,數據分析可結束。如p<0.05,表示此非線性系數具有統計學顯著性,數據組為非線性,此時應進行臨床標準的線性與非線性檢驗。
臨床標準的線性與非線性檢驗
上述多項式回歸分析主要是利用統計學方法進行線性判斷,統計學標準的線性可稱為一階線性,對數據組的要求很高。對于在臨床實驗室中使用的測定方法,在其臨床應用實踐中允許有一定的非線性誤差,此時通過對統計學標準的非線性作程度判斷,可得到臨床標準的線性,即二階線性。
臨床標準的線性檢驗中使用了兩個統計量,ADL(偏離直線平均差異,average deviation from linearity)與PctBnd(百分區界 ,percent bound) ,對于大多數分析物PctBnd取5%。如ADL小于所要求的臨界判斷值,則可認為數據組具有臨床可接受的線性,所擬合出的最適非線性多項式無臨床意義。
ADL值的計算:
ADL表示最優擬合曲線與直線的平均差異,其計算公式如下:
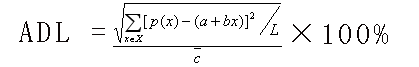
式中p(x)表示最優擬合二階或三階方程的擬合值,a+bx表示擬合一階方程的擬合值,L表示樣本數,c表示總平均濃度(全部測量數據的平均值)。
將ADL與臨界值比較
一般設定ADL小于5%為臨床允許誤差,即取PctBnd為5%,通過查表(見附表A與B)得到ADL臨界值。如ADL小于臨界值,可認為多項式具有臨床可接受的非線性,為二階線性。如ADL大于臨界值,則為臨床不可接受的非線性。
對數據組進行精密度檢驗
測量數據的精密度可直接影響多項式回歸分析的結果,為提高統計功效,需對數據組進行精密度檢驗。
計算最優擬合方程的回歸標準誤(σ)
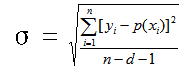
式中yi表示各個測量值,p(xi)表示最優擬合方程的擬合值,n表示樣本數乘以重復次數(L x R),d表示最優擬合方程的階數。
計算不精密度
用最優擬合方程的回歸標準誤(σ)與總平均濃度(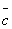 )的百分比代表不精密度。
)的百分比代表不精密度。
數據組的不精密度檢驗
跟據以下公式進行判斷:
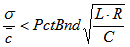
式中σ表示最優擬合方程的回歸標準誤,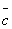 表示總平均濃度,L表示樣本數,R表示重復測量的次數,C表示常數(附表C),PctBnd:取5%。
表示總平均濃度,L表示樣本數,R表示重復測量的次數,C表示常數(附表C),PctBnd:取5%。
不精密度滿足判斷式時, 說明數據的精密度好可作線性評價。反之則表示數據的精密度差,不能作線性評價。當PctBnd取5%時, 尚可通過查不精密度和臨界值表判斷數據是否精密 (附表A和B), 如此時不精密度對應的臨界值顯示P, 表明測量數據的精密度不符合作線性判斷的要求。
結果報告
線性范圍報告的具體格式不要求,但至少應包括以下幾方面:
進行線性評價的實驗室或生產廠家名稱。
被評價的方法或試劑名稱,批號。
測定項目。
線性范圍(如為二階線性應包括臨床允許誤差)。
如可能應標出測定項目的醫學決定水平及在此水平處的臨床允許誤差。
附錄:
表A:不精密度和ADL的臨界值(PctBnd=5%,d=1或2階)
| σ/% | L*R=10 | L*R=12 | L*R=14 | L*R=16 | L*R=18 | L*R=20 |
| 1 | 5.5 | 5.5 | 5.4 | 5.4 | 5.4 | 5.4 |
| 2 | 6.1 | 6.0 | 5.9 | 5.8 | 5.8 | 5.7 |
| 3 | 6.6 | 6.4 | 6.3 | 6.3 | 6.2 | 6.1 |
| 4 | 7.1 | 6.9 | 6.8 | 6.7 | 6.6 | 6.5 |
| 5 | 6.6 | 7.4 | 7.2 | 7.1 | 7.0 | 6.9 |
| 6 | 8.2 | 7.9 | 7.7 | 7.5 | 7.4 | 7.2 |
| 7 | 8.7(P) | 8.4(P) | 8.1 | 7.9 | 7.8 | 7.6 |
| 8 | P | P | 8.6(P) | 8.3(P) | 8.1 | 8.0 |
| 9 | P | P | P | P | 8.5(P) | 8.3(P) |
| >9 | P | P | P | P | P | P |
L*R:樣本數*重復測量的次數
表B:不精密度和ADL的臨界值(PctBnd=5%,d=3階)
| σ/% | L*R=10 | L*R=12 | L*R=14 | L*R=16 | L*R=18 | L*R=20 |
| 1 | 5.5 | 5.5 | 5.4 | 5.4 | 5.4 | 5.4 |
| 2 | 6.1 | 6.0 | 5.9 | 5.9 | 5.8 | 5.8 |
| 3 | 6.7 | 6.5 | 6.4 | 6.3 | 6.2 | 6.2 |
| 4 | 7.2 | 7.0 | 6.9 | 6.8 | 6.7 | 6.6 |
| 5 | 7.8 | 7.6 | 7.4 | 7.2 | 7.1 | 7.0 |
| 6 | 8.4 | 8.1 | 7.9 | 7.7 | 7.5 | 7.4 |
| 7 | 9.0(P) | 8.7(P) | 8.4 | 8.2 | 8.0 | 7.8 |
| 8 | P | P | 8.9(P) | 8.6(P) | 8.4 | 8.2 |
| 9 | P | P | P | P | 8.9(P) | 8.7(P) |
| >9 | P | P | P | P | P | P |
L*R:樣本數*重復測量的次數
表C:不精密度界值的常數
| 最優擬合方程的階數 | 精密度界值的常數(C) |
| 一階或二階 | 6.3 |
| 三階 | 6.5 |

相關產品



 蘇公網安備32011202001302
蘇公網安備32011202001302